Return Model Assumptions
Highly sophisticated projections are a critical key to being able to do excellent financial planning. RightCapital uses advanced Monte Carlo simulations for all future-date predictions in the Retirement Analysis tool.
RightCapital's Monte Carlo simulations generate 1,000 return scenarios to illustrate potential paths for the client's financial future. The Monte Carlo simulation uses the global asset class returns, applied to the Asset Allocation model indicated in the Retirement Analysis Action Items.
Model Type
Our Legacy Monte Carlo simulation uses a stochastic volatility model often used in banks and life insurance companies to capture the dynamics of equity returns. The legacy model captures the complex dynamics of equity and bond modeling.
Our Standard Monte Carlo simulation uses the log-normal distribution model, which provides more flexibility when setting asset class returns and volatility assumptions. RightCapital will update the predefined assumption sets for asset class returns and volatilities annually.
Using the Standard model type, you can update your asset return assumptions with one of the three options:
Customized Returns
Historical Index Returns
Forward-Looking Assumptions (JP Morgan)
For more information on Asset Return Assumptions, please reference this Help Center article.
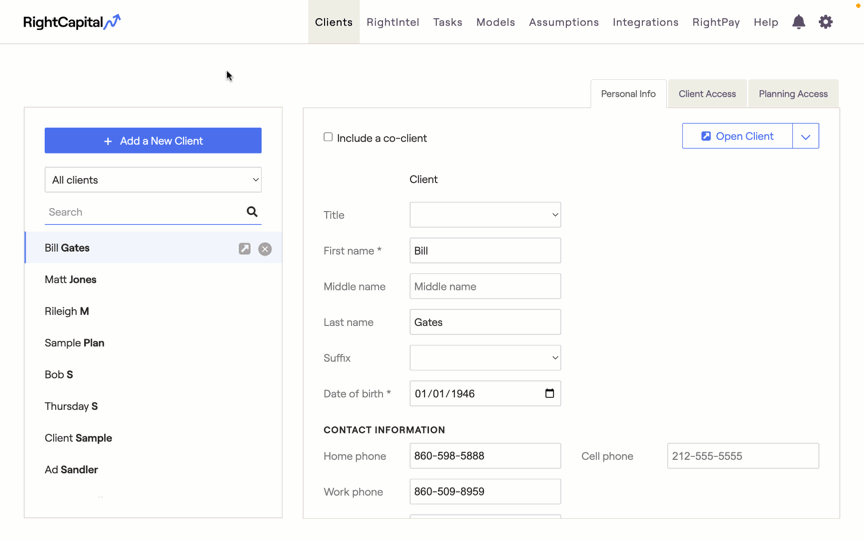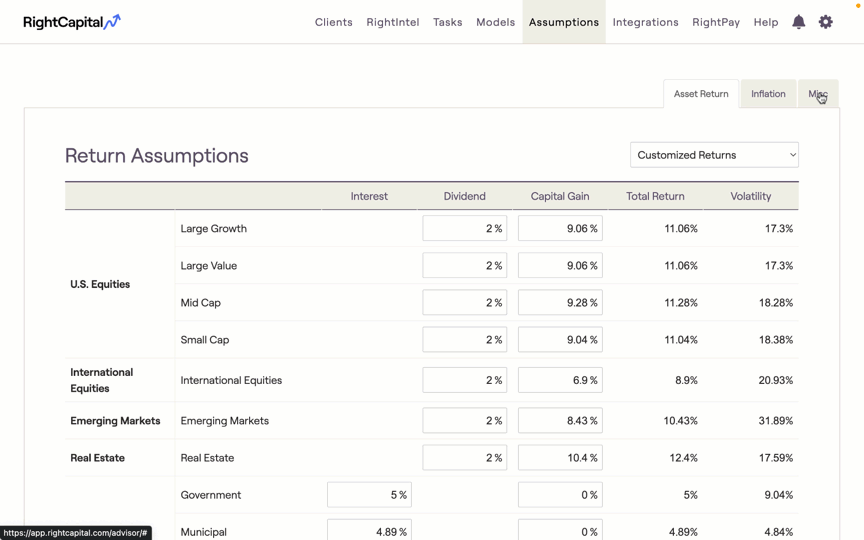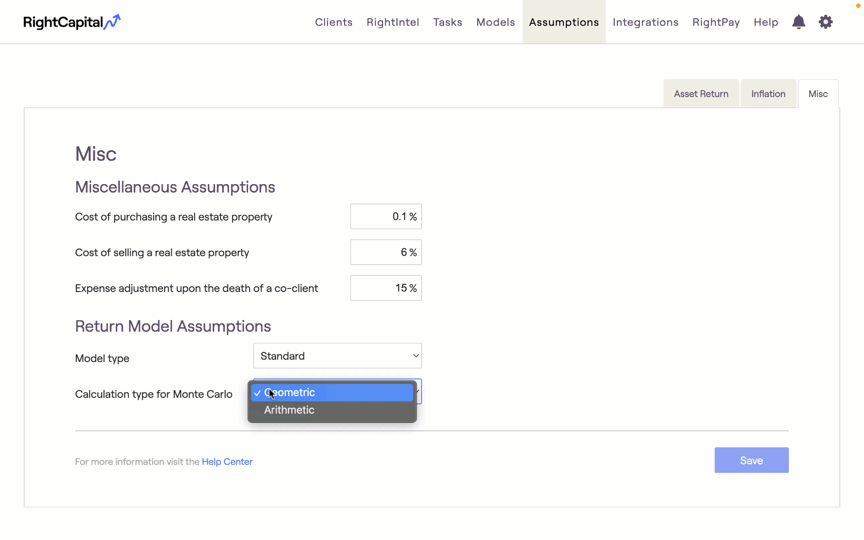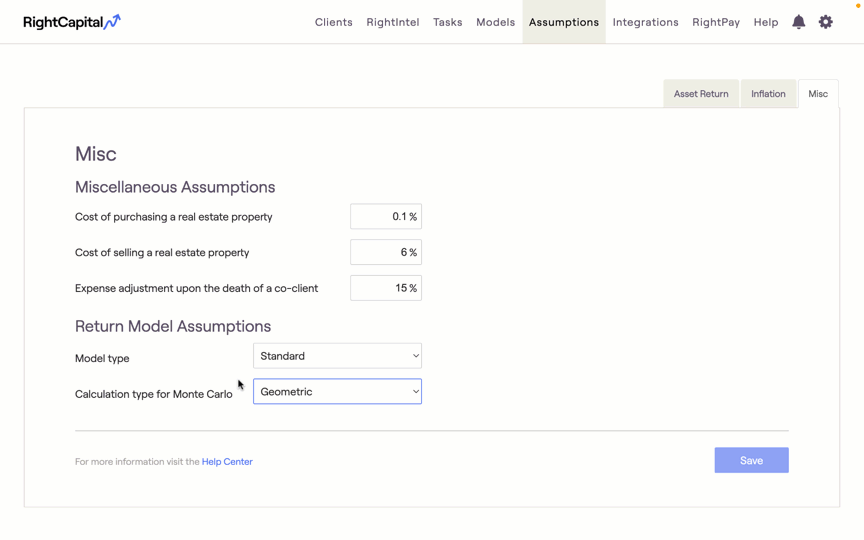
Calculation Type for Monte Carlo
Geometric - The geometric mean looks at the cumulative return over a period of time, factoring in the compounding effect of year-over-year returns.
Arithmetic - An Arithmetic mean takes the sum of the annual return numbers and divides that sum by the count of numbers used.
When the Calculation type is changed from Geometric to Arithmetic, we will see a small to modest increase in the probability of success for households. This could happen because the arithmetic calculation uses higher returns in the Monte Carlo simulation. A greater change will likely be seen for clients with a more volatile portfolio.
Custom Asset Classes
For advisors using Custom Asset Class capabilities, a slightly different model is used. This is due to the immense power of utility RightCapital places in the hands of these advisors, including the ability to update standard deviation/correlation assumptions. This granular approach utilizes a standard log-normal distribution model since we're factoring in the manually input asset class volatilities and correlations.